标题：Limits of Brownian trees with exponential weight on the height

报告时间：2025年8月13日（星期三）10：00-11：00

报告地点：人民大街校区数学与统计学院523报告厅

主讲人：何辉

主办单位：数学与统计学院

报告内容简介：

We consider a Brownian continuum random tree τ and its local time process at level s, say Zs, which evolves as a Feller branching diffusion. Denote by H(τ) and N the height and the law of the tree τ, respectively. Let μ ∈ R be a constant. We show that as r → ∞,

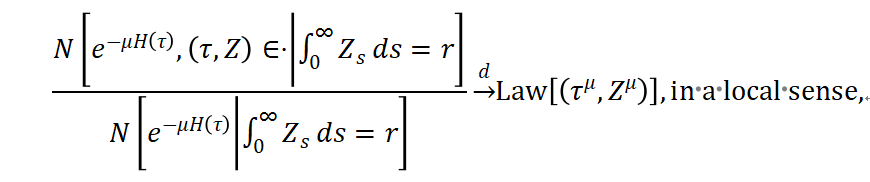
where if μ < 0, then τμ is a Kesten tree and if μ > 0, then τμ is the so-called Poisson tree constructed in Abraham, Delmas and He (2022, arXiv) by studying the local limits of τ. Moreover, Zμ is the local time process of τμ, which is a new diffusion, as already proved by Overbeck in 1994 by studying the Martin boundary of Z. We give a new representation of this diffusion using an elementary SDE with a Poisson immigration. The talk is based on some ongoing works with Romain Abraham, Jean-François Delmas and Meltem Ünel.

主讲人简介：

何辉，北京师范大学教授。2003年本科毕业于安徽大学，2008年博士毕业于北京师范大学，2009-2010年在法国奥尔良大学做博士后。主要从事与概率论有关的教学和科研工作。